Wiskunde trucs
Procentsom omdraaien
- 32% van 5 = 5% van 32
- 20% van 75 = 75% van 20
- 40% van 125 = 125% van 40
Reeks kwadraten van gehele getallen
Om bij de reeks kwadraten van gehele getallen (4, 9, 16, 25, 36, 49, ...) het volgende getal te vinden, tel je 2 keer het basisgetal plus 1 er bij op.
- 6² = 36
36 + (2 x 6) + 1
7² = 49
- 12² = 144
144 + (2 x 12) + 1
13² = 169
- 25² = 625
625 + (2 x 25) + 1
26² = 676
Kwadraten van n½
Het kwadraat van een geheel getal n plus een half is de som van n x (n+1) + ¼
- (2½)² = 2 x 3 + ¼ = 6¼
- (6½)² = 6 x 7 + ¼ = 42¼
- (43½)² = 43 x 44 + ¼ = 1892¼
Product van 11
Om een getal van twee cijfers te vermenigvuldigen met 11 tel je de twee cijfers bij elkaar op en plaats je die tussen de twee cijfers.
- 24 x 11
2 + 4 = 6
2 6 4
24 x 11 = 264
- 61 x 11
6 + 1 = 7
6 7 1
61 x 11 = 671
- 77 x 11
7 + 7 = 14
7 14 7
77 x 11 = 847
Tafel van 9
- Schrijf onder elkaar de cijfers van 0 t/m 9
- Schrijf rechts daarvan onder elkaar de cijfers 9 t/m 0
- 1 x 9 = 0 9
2 x 9 = 1 8
3 x 9 = 2 7
4 x 9 = 3 6
5 x 9 = 4 5
6 x 9 = 5 4
7 x 9 = 6 3
8 x 9 = 7 2
9 x 9 = 8 1
10 x 9 = 9 0
Tafel van 99
- Schrijf onder elkaar negen keer 9
- Schrijf links daarvan onder elkaar de cijfers 0 t/m 9
- Schrijf helemaal rechts onder elkaar de cijfers 9 t/m 0
|
1 x 99 = 0 9 9
2 x 99 = 1 9 8
3 x 99 = 2 9 7
4 x 99 = 3 9 6
5 x 99 = 4 9 5
6 x 99 = 5 9 4
7 x 99 = 6 9 3
8 x 99 = 7 9 2
9 x 99 = 8 9 1
10 x 99 = 9 9 0
|
|
1 x 999 = 0 99 9
2 x 999 = 1 99 8
3 x 999 = 2 99 7
4 x 999 = 3 99 6
5 x 999 = 4 99 5
6 x 999 = 5 99 4
7 x 999 = 6 99 3
8 x 999 = 7 99 2
9 x 999 = 8 99 1
10 x 999 = 9 99 0
|
|
1 x 9999 = 0 999 9
2 x 9999 = 1 999 8
3 x 9999 = 2 999 7
4 x 9999 = 3 999 6
5 x 9999 = 4 999 5
6 x 9999 = 5 999 4
7 x 9999 = 6 999 3
8 x 9999 = 7 999 2
9 x 9999 = 8 999 1
10 x 9999 = 9 999 0
|
Opvolgende getallen optellen
|
1 + 2 + 3 + 4 + ... + 20
1 + 20 = 21
2 + 19 = 21
3 + 18 = 21
4 + 17 = 21
...
10 + 11 = 21
Totaal 20/2 = 10 getalparen
Totaalsom: 10 x 21 = 210
|
|
1 + 2 + 3 + 4 + ... + 76
1 + 76 = 77
2 + 75 = 77
3 + 74 = 77
4 + 73 = 77
...
38 + 39 = 77
Totaal 76/2 = 38 getalparen
Totaalsom: 38 x 77 = 2926
|
|
1 + 2 + 3 + 4 + ... + 432
1 + 432 = 433
Totaal 432/2 = 216 getalparen
Totaalsom: 216 x 433 = 93.528
|
Zes decimalen van Pi onthouden
- onthoud de zin “How I wish I could calculate Pi”
- tel het aantal letters per woord
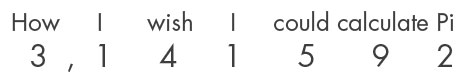
Alternatieven:
- Wow, I made a great discovery! (3.14159)
- Can I have a small container of coffee? (3.1415926)
- How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics. (3.14159265358979)
Vermenigvuldigen met grote getallen dicht bij 100
Bereken bij het vermenigvuldigen van de twee getallen eerst de twee linkse cijfers en dan de twee rechtse cijfers.
- bereken het verschil tussen het eerste getal en 100
bereken het verschil tussen het tweede getal en 100
tel deze twee getallen op
bereken het verschil tussen dit getal en 100
dit zijn de eerste twee cijfers van het antwoord
- vermenigvuldig de eerste twee verschillen van de vorige berekening
dit zijn de laatste twee cijfers van het antwoord
97 x 96
100 - 97
100 - 96
3 + 4
100 - 7
3 x 4
97 x 96 |
=
=
=
=
=
=
|
3
4
7
93
12
93 12 |
|
93 x 98
100 - 93
100 - 98
7 + 2
100 - 9
7 x 2
93 x 98 |
=
=
=
=
=
=
|
7
2
9
91
14
91 14
|
|
88 x 95
100 - 88
100 - 95
12 + 5
100 - 17
12 x 5
88 x 95 |
=
=
=
=
=
=
|
12
5
17
83
60
83 60
|
Worteltrekken uit het hoofd
Je kunt uit het hoofd vrij nauwkeurig worteltrekken met een trucje.
- bepaal het gehele getal van de uitkomst
- bepaal het verschil tussen dit gehele getal in het kwadraat en het getal waarover je de wortel wilt berekenen
- de uitkomst is het gehele getal van stap 1 + het verschil van stap 2 / (twee keer het gehele getal van stap 1)
| wortel |
geheel |
kwadraat |
rest |
deler |
berekening |
uitkomst |
exact |
verschil |
| √ 19 |
4 |
4² = 16 |
19-16=3 |
2*4=8 |
4 3/8 |
4,38 |
4,36 |
0,02 |
| √ 41 |
6
|
6² = 36 |
41-36=5
|
2*6=12 |
6 5/12 |
6,42 |
6,40 |
0,02 |
| √ 75 |
8
|
8² = 64
|
75-64=11
|
2*8=16 |
8 11/16 |
8,69 |
8,66 |
0,03 |
| √ 131 |
11
|
11² = 121
|
131-121=10
|
2*11=22 |
11 10/22 |
11,45 |
11,45 |
0,00 |
| √ 3873 |
62
|
62² = 3844
|
3873-3844=29
|
2*62=124 |
62 29/124 |
62,23 |
62,23 |
0,00 |
Kwadraatpiramide
| 1² |
= |
1 |
| 11² |
= |
121 |
| 111² |
= |
12321 |
| 1111² |
= |
1234321 |
| 11111² |
= |
123454321 |
| 111111² |
= |
12345654321 |
| 1111111² |
= |
1234567654321 |
| 11111111² |
= |
123456787654321 |
| 111111111² |
= |
12345678987654321 |
SosCasToa
Een ezelsbruggetje voor het gebruik van sinus, cosinus en tangens is het woord SosCasToa.
- Sos: Sinus = overstaand / schuin
- Cas: Cosinus = aanliggend / schuin
- Toa: Tangens = overstaand / aanliggend
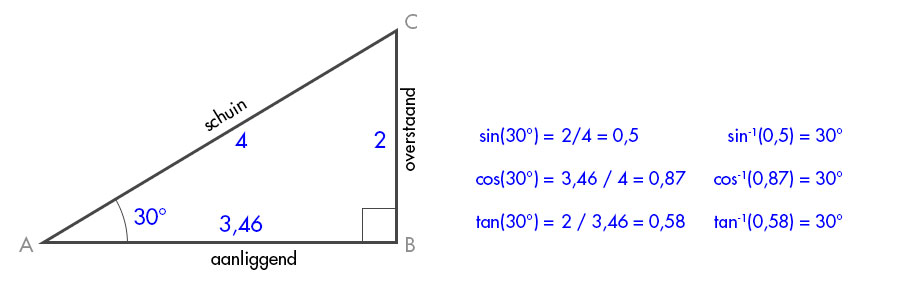
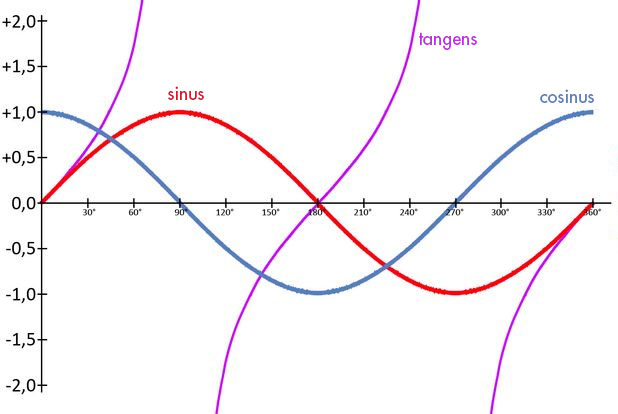
Sinus - Cosinus - Tangens
| sin(0°) = |
0 |
| sin(30°) = |
0,5 |
| sin(90°) = |
1 |
| sin(150°) = |
0,5 |
| sin(180°) = |
0 |
| sin(210°) = |
-0,5 |
| sin(270°) = |
-1 |
| sin(330°) = |
-0,5 |
| sin(360°) = |
0 |
|
| cos(0°) = |
1
|
| cos(30°) = |
0,5 |
| cos(90°) = |
0
|
| cos(150°) = |
-0,5 |
| cos(180°) = |
-1
|
| cos(210°) = |
-0,5 |
| cos(270°) = |
0
|
| oss(330°) = |
0,5 |
| cos(360°) = |
1
|
|
| tan(0°) = |
0
|
| tan(45°) = |
1
|
| tan(90°) = |
∞ |
| tan(135°) = |
-1 |
| tan(180°) = |
0
|
| tan(225°) = |
1 |
| tan(270°) = |
∞ |
| tan(315°) = |
-1
|
| tan(360°) = |
0
|
|
Pythagoras met mooie ronde getallen
Iedereen kent de stelling van Pythagoras: bij een driehoek met een rechte hoek geldt dat de som van de kwadraten van de zijden aan weerszijden van de rechte hoek, gelijk is aan het kwadraat van de overstaande, schuine zijde. a² + b² = c²
De meeste mensen kennen ook wel het magische trio 3/4/5
De wiskundige term hiervoor is primitieve pythagorese drieling.
Ook veelvouden voldoen aan de stelling: 6/8/10, 9/12/15, 30/40/50
Onder de 100 zijn er maar liefst 16 verschillende primitieve pythagorese drielingen:
| 3/4/5 |
3² + 4² = 5² |
9 + 15 = 25
|
| 5/12/13 |
5² + 12² = 13² |
25 + 144 = 169
|
| 8/15/17 |
8² + 15² = 17² |
64 + 225 = 289
|
| 20/21/29 |
20² + 21² = 29² |
400 + 441 = 841
|
| 12/35/37 |
12² + 35² = 37² |
144 + 1225 = 1369
|
| 9/40/41 |
9² + 40² = 41² |
81 + 1600 = 1681
|
| 28/45/53 |
28² + 45² = 53² |
784 + 2025 = 2809
|
| 11/60/61 |
11² + 60² = 61² |
121 + 3600 = 3721
|
| 16/63/65 |
16² + 63² = 65² |
256 + 3969 = 4225
|
| 33/56/65 |
35² + 56² = 65² |
1089 + 3136 = 4225
|
| 48/55/73 |
48² + 55² = 73² |
2304 + 3025 = 5329
|
| 13/84/85 |
13² + 84² = 85² |
169 + 7056 = 7225
|
| 36/77/85 |
36² + 77² = 85² |
1296 + 5929 = 7225
|
| 39/80/89 |
39² + 80² = 89² |
1521 + 6400 = 7921
|
| 65/72/97 |
65² + 72² = 97² |
4225 + 5184 = 9409
|
Band om de aarde
De omtrek van de aarde is ongeveer 40.000 km. Stel je voor dat je een band kunt aanbrengen strak om de aarde. Stel je voor dat je die band dan met 10 meter verlengt en de speling die ontstaat gelijk verdeelt over de gehele omtrek, hoeveel is dan die speling? Is er voldoende speling om er een muis onderdoor te laten lopen?
| omtrek aarde: |
40.000 |
km |
| omtrek aarde: |
40.000.000 |
m |
| diameter aarde: |
40.000.000 / π
|
m |
| diameter aarde: |
12.732.395,45 |
m |
| straal aarde: |
6.366.197,72 |
m |
|
| verlengde band: |
40.000.010 |
m |
| diameter band: |
40.000.010 / π
|
m |
| diameter band: |
12.732.398,63 |
m |
| straal band: |
6.366.199,32 |
m |
|
speling:
|
1,59 |
m |
